Linear Momentum of a System of Particles

A body of mass 5 kg explodes at rest into three fragments with masses in the ratio 1 : 1 : 3. The fragment with equal masses fly in mutually perpendicular directions with speeds of 21 ms^-1​. The velocity of heaviest fragment in ms^-1 will be

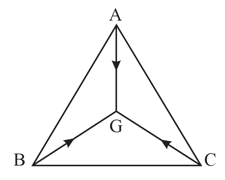
Three particles $A, B$ and $C$ of equal mass move with equal speed $v$ along the medians of an equilateral triangle as shown in figure. They collide at the centroid $G$ of the triangle. After the collision, $A$ comes to rest, $B$ retraces its path with the speed $V$. What is the velocity of $C$?

A nucleus disintegrates into two nuclear parts which have their velocities in the ratio $2:1$. The ratio of their nuclear sizes will be

A man throws a ball straight up. The ball has a momentum in the vertically upward direction.The principle of conservation of momentum demands that the earth has

Two balls having linear momenta ${\overrightarrow{p}}_1=p\hat{\mathrm{i}}$ and ${\overrightarrow{p}}_2=-p\hat{\mathrm{i}}$, undergo a collision in free space. There is no external force acting on the balls. Let ${\overrightarrow{p}}_1^{\text{'}}$ and ${\overrightarrow{p}}_2^{\text{'}}$ be their final momenta. The following option (s) is (are) not allowed for any non-zero value of $p, a_1, a_2, b_1, b_2, c_1$ and $c_2$.

A man of mass $50 \mathrm{kg}$ is standing at one end of a boat of length $25 \mathrm{m}$ and mass $200 \mathrm{kg}$. He starts running and when he reaches the other end, he has a velocity $2{ \mathrm{ms}}^{-1}$ with respect to the boat. The final velocity of the boat is (in ${\mathrm{ms}}^{-1}$)

A shell of mass $10 \mathrm{kg}$ is moving with a velocity of $10{ \mathrm{m} \mathrm{s}}^{-1}$ when it blasts and forms two parts of mass $9 \mathrm{kg}$ and $1 \mathrm{kg}$ respectively. If the 1st mass is stationary, the velocity of the $2\mathrm{nd}$ is

A ball of mass $0.2 \mathrm{kg}$ rests on a vertical post of height $5 \mathrm{m}$. A bullet of mass $0.01 \mathrm{kg}$, travelling with a velocity $v \mathrm{m}/\mathrm{s}$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $20 \mathrm{m}$ and the bullet at a distance of $100 \mathrm{m}$ from the foot of the post. The initial velocity $v$ of the bullet is

A shell is fired from a cannon with a velocity $v$ $\left(\mathrm{m} {\mathrm{s}}^{-1}\right)$  at an angle $\theta$ with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. One of the pieces retraces its path to the cannon with speed $v \cos \theta$ then the speed (in $\mathrm{m} {\mathrm{s}}^{-1}$) of the other piece immediately after the explosion is

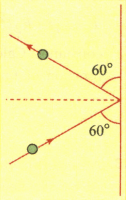
A $3 \mathrm{kg}$ ball strikes a heavy rigid wall with a speed of $10 \mathrm{m}/\mathrm{s}$ at an angle of $60°$ with the wall. It gets reflected with the same speed at $60°$ as shown in Fig.If the ball is in contact with the wall for $0.2 \mathrm{s}$, the average force on the ball by the wall is:

A stationary body explodes into four identical fragments such that three of them fly off mutually perpendicular to each other, each with a kinetic energy $\frac{E_0}{2}$ . The total energy of explosion is

A bullet of mass $m$ moving with velocity $v$ is fired into a wooden block of mass $M$. If the bullet remains embedded in the block, the final velocity of the system is

The momentum of a body is increased by $25\mathrm{\%}$. The kinetic energy is increased by about $56\%$.

In the non-relativistic regime, if the momentum is increased by $100\%,$ the percentage increase in kinetic energy is (in $\%$)

A gun fires a shell and recoils horizontally. If the shell travels along the barrel with speed $v$, then what is the ratio of speed with which the gun recoils if $\left(\mathrm{i}\right)$ the barrel is horizontal $\left(\mathrm{ii}\right)$ inclined at an angle of $30°$ with horizontal?

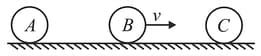
Three balls $A\text{,} B$ and $C$ $\left(m_{\mathrm{A}}=m_{\mathrm{C}}=4m_{\mathrm{B}}\right)$ are placed on a smooth horizontal surface. The ball $B$ collides with the ball $C$ with an initial velocity $\nu$ as shown in the figure. The total number of collisions between the balls will be (all collisions are elastic),

A ball of mass $0.2 \mathrm{kg}$ rests on a vertical post of height $5 \mathrm{m}$. A bullet of mass $0.01 \mathrm{kg}$, traveling with a velocity $\nu \mathrm{m}/\mathrm{s}$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $20 \mathrm{m}$ and the bullet at a distance of $100 \mathrm{m}$ from the foot of the post. The initial velocity $\nu$ of the bullet is

Find the speed of the daughter nucleus when a nucleus of ${}_{84}\mathrm{X}^{220}$ originally at rest emits an $\alpha$-particle with speed $v_0.$

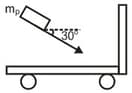
A cart is initially at rest and may roll freely. A $10 \mathrm{kg}$ package drops into a $25 \mathrm{kg}$ cart with a velocity of $3 \mathrm{m}/\mathrm{s}$. Determine  $\left(a\right)$ the final velocity of the cart, $\left(b\right)$ the impulse exerted by the cart on the package, $\left(c\right)$ the fraction of the initial energy lost in the impact.